Co to jest rekurencja w PHP oraz jakie są przykłady jej użycia?

30.03.2023

Rekurencja jest jedną z podstawowych koncepcji programowania, która pozwala na zastosowanie w kodzie powtarzających się wzorców. W PHP jest nie tylko możliwa, ale również bardzo przydatna w pewnych przypadkach. W tym artykule omówimy, czym jest rekurencja w PHP, przykłady jej użycia oraz kiedy warto z niej korzystać, a kiedy lepiej zrezygnować.

Czym jest rekurencja w PHP?

Rekurencja w PHP oznacza wywoływanie funkcji przez samą siebie. Funkcja robi to aż do momentu, kiedy zostanie spełniony warunek zakończenia. W ten sposób tworzone są drzewa wywołań, gdzie każde kolejne wywołanie funkcji tworzy nową gałąź. Rekurencja często jest używana do operacji na złożonych tablicach lub do rozwiązywania matematycznych funkcji, z przykładami których możemy zapoznać się poniżej.

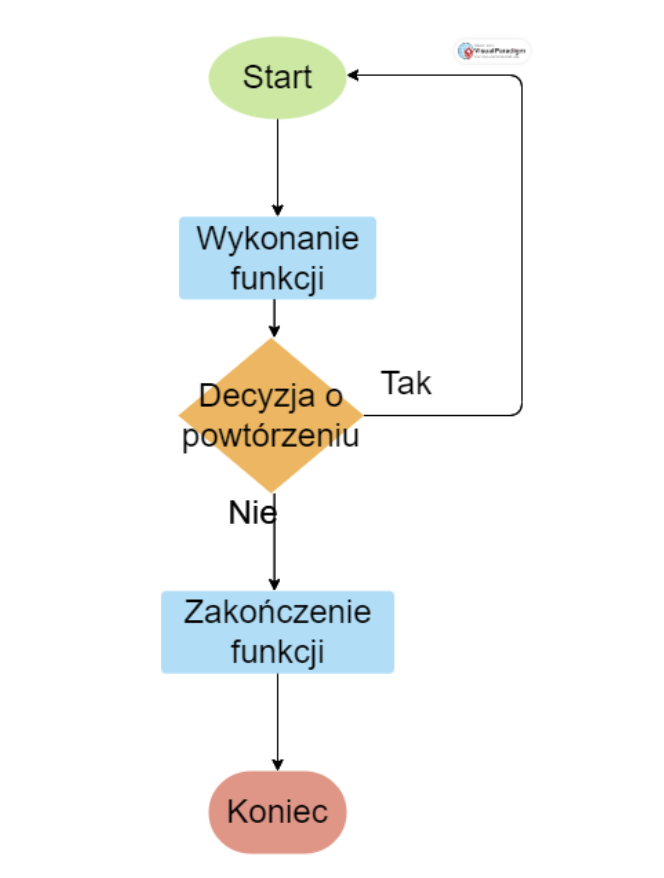
Przykłady rekurencji w PHP

Poniżej przedstawiamy kilka zastosowań rekurencji w praktyce.

Funkcja obliczająca silnię

Funkcja obliczająca silnię to jedna z najprostszych funkcji wykorzystujących rekurencję w PHP. Silnia liczby n jest definiowana jako iloczyn wszystkich liczb naturalnych mniejszych lub równych n.

function silnia($n) {
  if ($n <= 1) {
    return 1;
  }
  else {
    return $n * silnia($n - 1);
  }
}

Funkcja ta sprawdza, czy argument $n jest mniejszy lub równy 1. Jeśli tak - zwraca wartość 1. W przeciwnym przypadku, funkcja wywołuje samą siebie z argumentem zmniejszonym o 1 i mnoży ten argument przez wartość zwróconą przez kolejne wywołanie funkcji. Ten proces kontynuuje się, aż argument osiągnie wartość 1, co kończy rekurencję.

Funkcja obliczająca n-ty wyraz ciągu Fibonacciego

Ciąg Fibonacciego to ciąg liczb naturalnych, w którym każdy kolejny wyraz jest sumą dwóch poprzednich.

function fibonacci($n) {
  if ($n == 0 || $n == 1) {
    return $n;
  }
  else {
    return fibonacci($n - 1) + fibonacci($n - 2);
  }
}

Warunek if sprawdza, czy argument $n jest równy 0 lub 1. Jeśli tak, funkcja zwraca wartość argumentu. W przeciwnym przypadku funkcja wywołuje samą siebie z argumentami zmniejszonymi o 1 i 2, aż osiągnie wartości indeksów równych 0 lub 1.

Funkcja wyświetlająca wszystkie kombinacje znaków

Funkcja ta przyjmuje dwa argumenty - łańcuch znaków $prefix oraz łańcuch znaków $rest. Funkcja wyświetla wszystkie kombinacje łańcucha $prefix z każdą możliwą kombinacją łańcucha $rest. Implementacja tej funkcji wygląda następująco:

function kombinacje($prefix, $rest) {
  $n = strlen($rest);
  if ($n == 0) {
    echo $prefix . "<br>";
  }
  else {
    for ($i = 0; $i < $n; $i++) {
      kombinacje($prefix . $rest[$i], substr($rest, 0, $i) . substr($rest, $i + 1, $n - $i -1));
    }
  }
}

Funkcja ta wykorzystuje rekurencję oraz pętlę for do wyświetlenia wszystkich kombinacji łańcucha $prefix z każdą możliwą kombinacją łańcucha $rest. Warunek if w funkcji sprawdza, czy łańcuch $rest jest pusty. Jeśli tak, funkcja wyświetla łańcuch $prefix. W przeciwnym przypadku, funkcja wywołuje samą siebie, przekazując jako argumenty $prefix z dodanym znakiem z łańcucha $rest oraz pozostałą część łańcucha $rest, bez dodanego znaku.

Kiedy warto zastosować rekurencję?

Rekurencja jest przydatna wtedy, gdy problem można łatwo podzielić na mniejsze części, a każda z tych części jest rozwiązywalna w sposób podobny do pierwotnego problemu. Rekurencyjne podejście do rozwiązywania problemów jest szczególnie przydatne, kiedy problem ma strukturę drzewa lub grafu. W naszych przykładach przedstawiliśmy jej prostsze zastosowania. Jednak jest też używana w następujących przypadkach:

Algorytmy dziel i zwyciężaj, takie jak sortowanie szybkie i algorytm Mergesort.
Wyszukiwanie ścieżki w grafie albo drzewie, np. algorytm przeszukiwania w głąb (DFS) lub przeszukiwania wszerz (BFS).
Generowanie ciągów, takich jak ciągi Fibonacciego albo liczb pierwszych.
Obliczanie wartości funkcji matematycznych, które zależą od wcześniejszych wartości funkcji, np. silnia lub liczby Bernoulliego.
Tworzenie drzewa rekurencyjnego, np. drzewa genealogicznego lub binarnego.

Warto jednak pamiętać, że zbyt duża liczba wywołań rekurencyjnych może prowadzić do przekroczenia stosu, co prowadzi do błędu przepełnienia stosu (stack overflow error). Dlatego ważne jest odpowiednie zdefiniowanie warunków końcowych rekurencji oraz ograniczenie liczby wywołań.

Kiedy nie stosować rekurencji?

Rekurencja jest potężnym narzędziem programistycznym, które pozwala na rozwiązywanie złożonych problemów w elegancki i efektywny sposób. Jednakże istnieją pewne sytuacje, w których użycie rekurencji nie jest najlepszym rozwiązaniem.

Po pierwsze rekurencja może prowadzić do bardzo głębokich i skomplikowanych stosów wywołań. To z kolei może skutkować przekroczeniem dostępnej pamięci i spowodować błąd pamięci. W takich sytuacjach lepiej jest zastąpić rekurencję iteracyjną pętlą.

Kolejnym przypadkiem jest wydajność. Rekurencja często wymaga wielu wywołań funkcji, co może prowadzić do znacznego spadku wydajności. W przypadku gdy wydajność jest kluczowa, należy rozważyć użycie innych technik programistycznych, takich jak programowanie dynamiczne lub metoda podziału i zwyciężania.

Inną sytuacją, w której rekurencja może nie być najlepszym rozwiązaniem, jest trudność w zrozumieniu kodu. Głęboko zagnieżdżone wywołania rekurencyjne mogą sprawić, że kod staje się trudny do zrozumienia i utrzymania. W takich sytuacjach lepiej jest użyć prostszych technik programistycznych, takich jak petla while lub foreach, które są łatwiejsze do zrozumienia.

Rekurencja może nie być najlepszym rozwiązaniem również w przypadku, gdy problem można rozwiązać w prostszy sposób za pomocą innych technik programistycznych. W niektórych sytuacjach, na przykład w przypadku problemów geometrycznych, lepiej jest użyć innych metod, takich jak geometria analityczna.

Anegdota

Jedną z ciekawszych anegdot o rekurencji, opartą na faktach, jest historia związana z popularnym algorytmem sortowania nazywanym Quicksort. Według legendy, jego twórca, Sir Tony Hoare, popełnił błąd w implementacji i nie był w stanie znaleźć rozwiązania przez kilka godzin.

Ostatecznie Hoare zauważył, że jego algorytm był rekurencyjny i popełnił błąd w jednym z przypadków bazowych. Dlatego skupił się na zmianie logiki kodu w tym przypadku bazowym, a następnie ponownie wywołał Quicksort. Po kilku chwilach algorytm zakończył działanie i działał poprawnie.

Ciekawostką jest, że Hoare sam nazwał ten incydent "największym błędem w jego karierze". Jednakże dzięki temu zdarzeniu poprawił on algorytm i jego metodykę programowania. Ta historia jest dziś przykładem tego, jak błędy w kodzie, nawet te związane z rekurencją, mogą prowadzić do rozwoju i doskonalenia algorytmów.

Rekurencja w PHP - podsumowanie

Rekurencja jest bardzo ważnym pojęciem w programowaniu, szczególnie w przypadku algorytmów i struktur danych. Jest to proces, w którym funkcja wywołuje samą siebie w celu rozwiązania problemu. Może pomóc w uproszczeniu kodu i zapobiec duplikacji, ale też prowadzić do problemów z wydajnością i bezpieczeństwem. Przed użyciem tej metody należy upewnić się, że jest najlepszą odpowiedzią na nasz problem. Za bardzo rozbudowane i wielokrotnie wywoływane funkcje mogą prowadzić do zmniejszenia czytelności kodu oraz zbyt mocno obciążyć serwer. Kluczowe jest więc sprawdzenie ich wydajności i logiki.

Jeśli spodobał Ci się artykuł, zapraszamy na naszego bloga po więcej wiedzy z branży IT!